Last time I described in principle how the ambient occlusion shader works, but didn't really go into the details. Today I'll go into a bit more detail.
Something that I think may not have been clear last time is that we're calculating ambient occlusion independently from lighting based on the "blocklight" and "skylight" values. For ambient occlusion we're considering only the arrangement of solid blocks in the immediate neighbourhood, not any genuine sources of light. As a separate step we later multiply together the ambient occlusion value and the light-level based on blocklight and skylight. Again, this is a simplification, and it does result in extra shadows in dark areas, but it generally looks fine.
As we saw previously, to determine the the level of shadow added by occlusion, we determine how much "sky" is visible from the rendered surface, where the sky is actually a horizontal square not very far above the surface. This screenshot shows the view from the ground looking up. The white blocks represent the sky square, and the stone slabs are neighbouring taller cells.
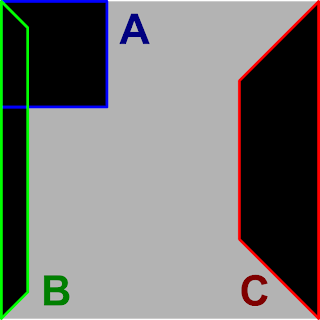
The yellow outline shows the unoccluded area of sky. The following diagram breaks that down into the areas shadowed by each of the eight neihbouring columns:
Area A is the occlusion from a neighbouring corner block, while areas B and C are occlusions from neighbouring side blocks. You'll observe that 1. the corner blocks always occlude rectangular regions of sky; 2. the side blocks occlude trapezoidal areas and 3. the corner block occlusions can overlap with the neighbouring side blocks.
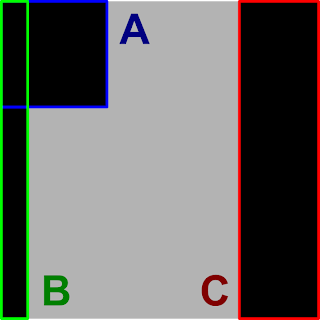
Now, I have to admit that I made a bit of a mistake when I first worked this out, and didn't realise that the side blocks were occluding trapezoids, so I worked it as if they were rectangles instead, like this diagram:
The problem with making this as a simplification is that it will result in significant discontinuities around corners. Encountering these, but not understanding why, I experimented with tweaking values and if you look in the shader code you'll see a comment, "TODO: Figure out why the 2* multiplier is needed in the next line!" I haven't actually figured out why that works yet, but I plan to work through the maths again with trapezoids, if it's not too complicated, and see how it compares. However, for now I'm going to discuss the slightly broken version with the rectangles.
Here's another pair of diagrams of those occlusion rectangles:
On the left we have a similar case with some extra occluding columns. Things to note here are that the yellow corner column provides no extra occlusion because it is shorter than both of the neighbouring side columns. The dotted line shows the division of the sky square into quadrants, each of which we'll handle separately.
On the right diagram, you can see the same arrangement, but different rectangles are highlighted. The orange "+" rectangle is the area of unoccluded sky in the quadrant ignoring the corner column. This can be easily calculated based on the proximity of the neighbouring cells on the sides, and the heights of the columns in those cells. The teal "−" rectangle is the extra occlusion provided by the corner column, which we subtract from the unoccluded area to find the total unoccluded area in the quadrant. We calculate the teal area similarly, using the proximity of the neighbouring side cells, and the height of the corner column, but we make sure to clamp its dimensions to be positive – if either dimension would be negative it means the corner block is not going to provide any occlusion and can be ignored.
I've left this a bit late, so I don't have formatted code snippets or a nice runnable example, but you can go look at the complete fragment shader in github. The obscurely named "lightcalc" calculates the dimension of one side of the orange rectangle based on the height and proximity of the neighbouring cell, with 1 being the maximum unoccluded size. "cornerlight" calculates the unoccluded area in the quadrant, again with 1 being entirely unoccluded.
This shader is pretty slow. It results in a noticeable frame-rate drop for me. I haven't yet investigated whether the cost is in the quantity of calculations or from sampling all eight neighbouring cells for their height, but I suspect it's the latter. If that's the case, we could preprocess the image and store information about each cell's neighbours in a compressed form, reducing the number of samples needed. Maybe an expert could suggest the most fruitful avenues to optimization.
Here's what it looks like without any textures:
Any thoughts? It occurs to me that I could very well have overlooked a much easier or a less horrifically simplified way to do this. I'll need to look into how feasible it is to properly calculate the trapezoidal areas, and also figure out why the bodge of doubling the teal area results in continous results (at least, continuous between cells of equal height; we don't want continuity across height changes – the whole point of this is to highlight height differences). Feel free to ask questions if it's not clear. I may yet do one more post on this topic if people would like further clarification.